Recently, Chinese scientists published a paper on new astronomy (96: 101850, 2022).Three-Body Problem – From Newton to Supercomputer Plus Machine Learning“Paper,Based on machine learning and a highly accurate numerical algorithm (CNS), a roadmap is proposed to solve the popular “three-body problem” periodic orbit.The first author of the article was Liao Shijun of Shanghai Jiotong University, the second author was Li Xiaoming of Jinan University, and the third author, Yang Yu, was a doctoral student at Shanghai Jiotong University.

How do three planets with any mass move under the force of gravity? The famous “three-body problem” proposed by Newton in 1687 has received widespread attention from the international academic community for over 300 years and has become one of the most famous scientific problems in history. According to the topological classification of the periodic orbits of the three-body problem proposed by Montgomery from 1687 to 1993, only three periodic orbital families of the three-body problem were found, namely: (1) Euler-Lagrange family (exact solution, Euler 1740, Lagrange 1772), (2). Family (Numerical Solution, Broucke 1975, Broucke and Boggs 1975, Hadjidemetriou 1975, Hénon 1976) (3) Figure-8 Family (Numerical Solution, Moore 1993). Why is it difficult to find periodic orbits of three body problems? In 1890, Poincaré discovered that the trajectory of a three-body system is generally not the first type (i.e., the analytical solution is generally non-existent) and is very sensitive to initial conditions: any slight disturbance. Expanding extensively, making its trajectory equal to one, rapid separation of original solutions. In 1963, Lawrence rediscovered the sensitivity of this path to minor disturbances and suggested the famous “butterfly effect”. The discovery of this character marks the birth of “anarchic dynamics”, considered one of the three greatest physical theories of the twentieth century, combined with quantum mechanics and relativity. The anarchic nature of the three-body problem made it difficult to obtain the exact orbit of the three-body system in the long-term domain, even using conventional numbering methods. More than 300 years after Newton introduced the three-body problem in 1687, it is well illustrated that only three periodic orbits of the three body problems have been discovered.

Everyone knows that there are errors in any number calculation. In 1989, Lawrence discovered that due to the “butterfly effect”, a small number error, as well as a small artificial disturbance, can cause a rapid change in the numerical resolution (path) of an anarchic system. In particular, Lawrence found that the path of a trouble-free system does not coincide, no matter how short the time frame, if a random dynamic system is numerically solved with double accuracy. In 2013, when computer performance reached the order of 10 billion petaflops, this explains why the three-body problem Family 11’s only discovered the new periodic orbits.

In 2009, Liao Shijun of Jiao Tong University in Shanghai proposed a strategy for numerically solving the Clean Numerical Simulation (CNS) of seamless dynamics. CNS not only reduces the summation error of the number simulation, but also uses multiple precision data (multiple precision) instead of double accuracy to unilaterally minimize the whole number error. The domain will be available for release in a timely manner. Thus, the CNS theoretically paves the way for accurate obtaining periodic orbits for three body problems. In 2017, Liao Shijun’s team successfully combined the CNS search method with the Newton-Raffson iteration method to successfully obtain 695 family periodic orbits of equal mass and zero angular momentum. (2017), 2013 saw the discovery of periodic orbits of 11 groups (with periods below 100) and 466 periodic orbits with periods greater than 100, including Suvakov and Dimitrazinovich, which were never reported. In 2018, Liao Shijun’s team collaborated with Jing Yipeng, an academic at the School of Physics and Astronomy at Shanghai Jiao Tong University, and applied the CNS, search methods and the Newton-Rafson iteration method to make the 1349 family’s two new cycles more successful. Three-body systems with equal mass and zero angular momentum. For the three-body problem of uncontrolled mass inequality, in 2021, Liao Shijun and Li Xiaoming will integrate the CNS with the complete method and the Newton-Rafson repetition method, starting from the known periodic orbit. Get the same mass, successfully, with different masses (Science China – Physics, Mechanics & Astronomy, 2021) There are 135,445 periodic solutions of the three body systems, increasing the number of periodic orbits of the three body problems. Through several magnitude sequences that confirm that the CNS can fix the periodic orbit of three body problems (especially long orbits). In contrast to the hierarchical structure of the Sun-Earth, many of these periodic orbits are orbiting the orbit of the solar system, which is similar to that of the Nobel Prize-winning mass eclipse. Discovered the first observable planet.

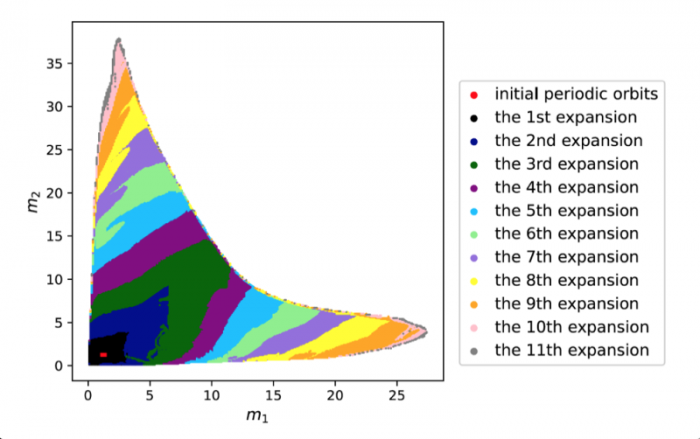
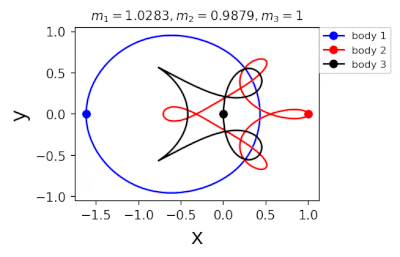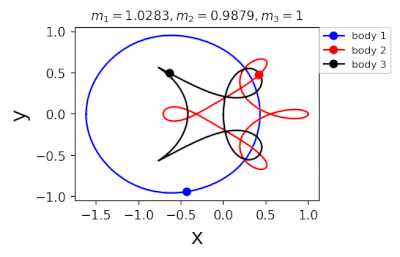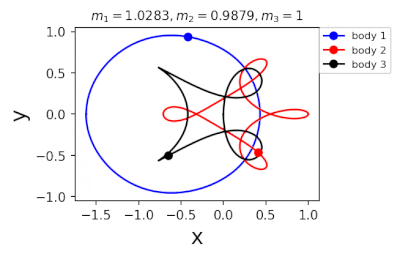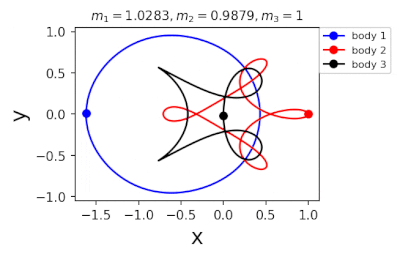
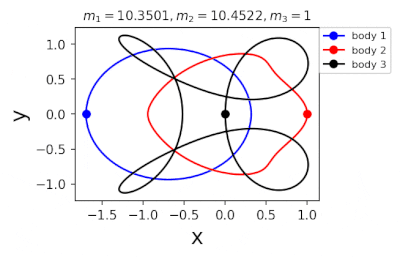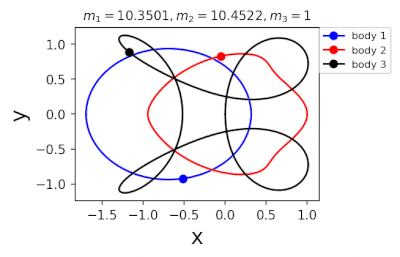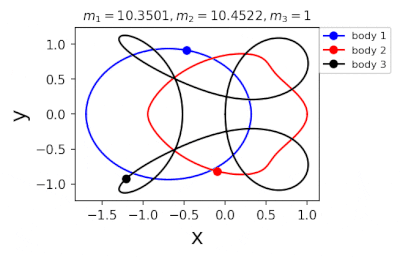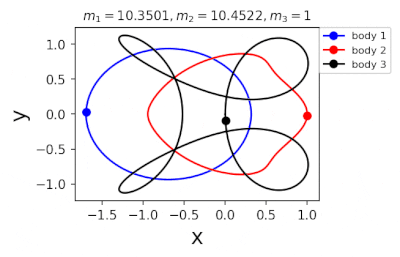
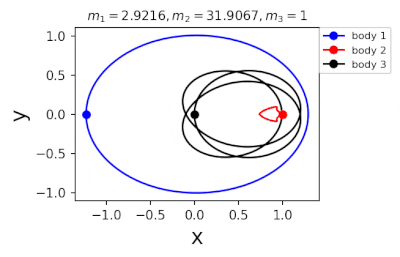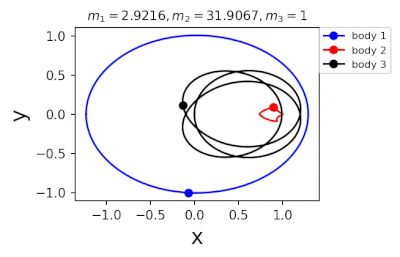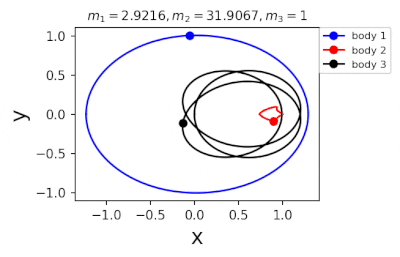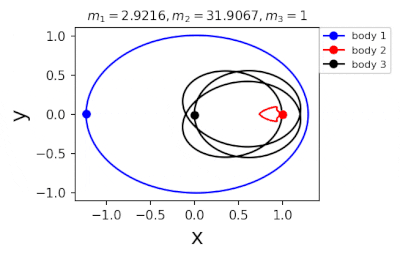
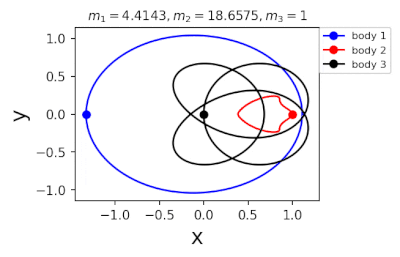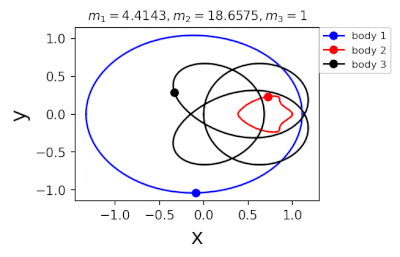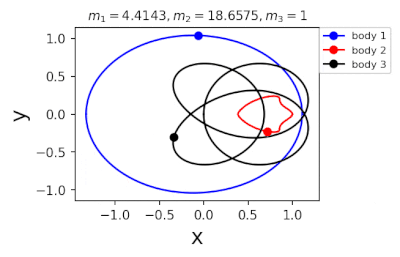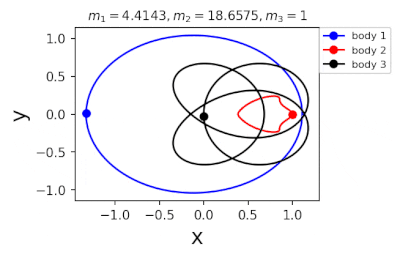
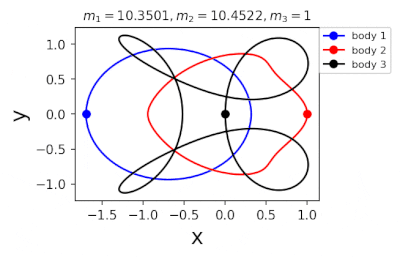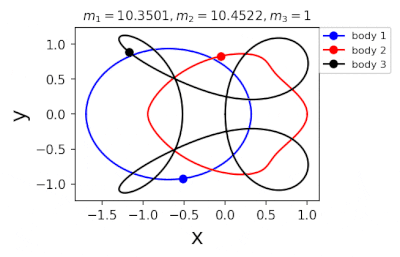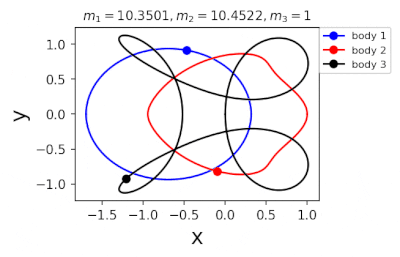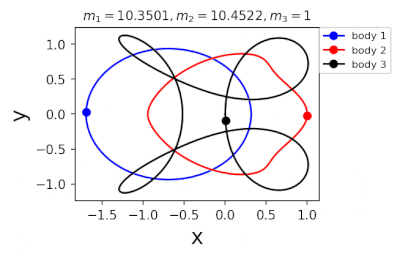
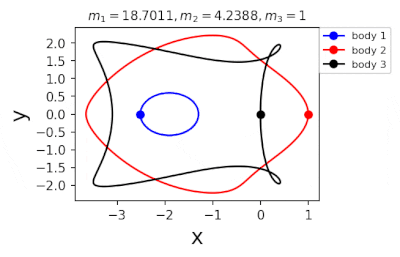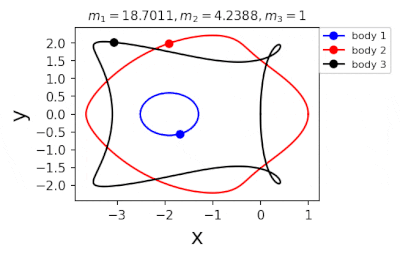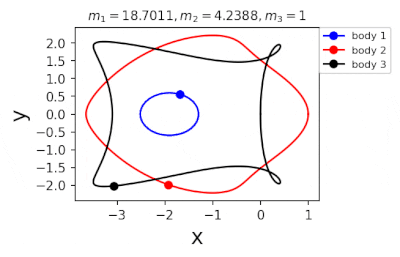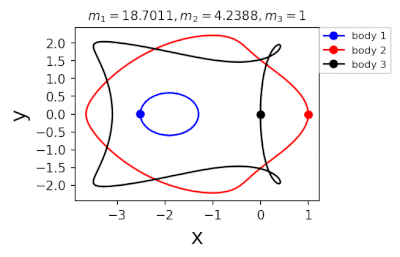
Figure 1: Machine learning is used to find the periodic orbits of different planetary masses in the same family of three body systems. The red area in the lower left corner is just a few periodic orbits obtained by conventional methods. The same color indicates the same extrapolation, the largest area of ​​periodic orbits that can be detected by machine learning. m1 and m2 are two planetary masses (m3 = 1).

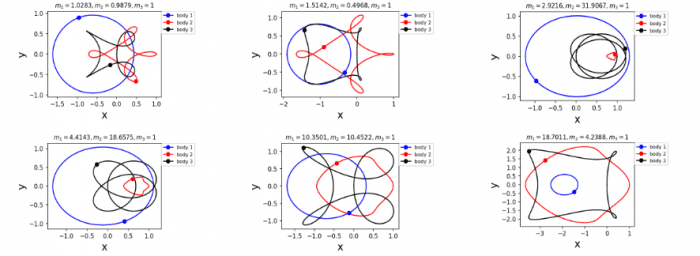
In 2022, Liao Shijun, Li Xiaoming and Yang Yu will combine CNS with machine learning and Newton-Rafson repetition to further improve computational efficiency. The estimated value of the initial conditions of the periodic orbits of the three bodies gives the problem of extrapolation of the star, and then the CNS is used to obtain the convergence path of the stellar motion with high accuracy, and Newton-Rafson sets the initial conditions for repeating its exact periodic orbit. All the new periodic orbits obtained through interpolation form a large training set, the extrapolation range of the planetary mass is continuously increased, and the prediction accuracy of the initial value of the periodic orbits is continuously improved by the machine learning model. Three physical problems of this family were found. Periodic orbits as shown in Figure 1. Finally, the machine learning model trained with all the periodic orbits obtained in this way can accurately predict the initial conditions, durations, and stability of the repetitive orbits (in the region where the periodic orbits exist), as shown in Figure 2. This CNS and machine learning-based strategy enhances computational efficiency in a number of ways, suggesting a completely new roadmap for efficiently obtaining periodic orbits for the three-dimensional problem. This paper will be published in the International Astronomical Journal of New Astronomy in 2022 (https://doi.org/10.1016/j.newast.2022.101850), and related machine learning programs and periodical orbits are available on GitHub (https: // gith). sjtu-liao / three-body) for free download.

Thanks to the use of the CNS, the (non-dimensional) periodic orbit achieved by Liao Shijun’s team and their collaborators achieves an effective accuracy of 60 bits: even at the characteristic length of the cosmic diameter (930 light-years). ), The accuracy of its starting position reaches 1.0E-41 m, which is much less than the minimum length of physical significance – the plank length (1.62E-35 m). Therefore, from a physical point of view, it does not make sense to further improve the accuracy of the computational results, although this is easily done with the CNS. Therefore, the accuracy of the periodic orbit of the three-body problem achieved by the CNS is very high, which is the exact orbit in the physical sense. In other words, physically speaking, the exact solution of the periodic orbit of the three body problems can be obtained by applying the CNS!

Liao Shijun, Li Xiaoming, and Yang Yu proposed a roadmap for solving the periodic orbit of the trinity problem based on the CNS and machine learning, which improved computational efficiency in a number of ways and paved the way for greater (physically) attainment. ) Level the road with accurate periodic orbits for three body problems. Today, with the availability of high-performance computers, there is no barrier to preventing mankind from achieving the colossal (physically) accurate periodic orbits of the three-body problem. The solution to the three-body problem depends largely on high-performance computers and mathematical methods. Looking back over 300 years of solving the famous problem of the “three body problem”, one cannot help but thank those great mathematicians, physicists, and engineering technologists, especially those who created “chaotic dynamics”, computers, and Turing. , Von Newman, the father of artificial intelligence, the architect of modern computers, and Jack S., winner of the 2000 Nobel Prize in Physics for his discovery of integrated circuits. The solution to the classic puzzle of the periodic orbit of the three-body problem is a model of a combination of theory and technology.

The solution of the periodic orbit of the three-body problem demonstrates the effectiveness and potential of the CNS in solving complex problems. Theoretically, the CNS could be applied to the solution of periodic orbits of N-body problems (N> 3), the exact numerical simulation of galactic evolution, and the exact numerical simulation of turbulence.

Figure 2: Periodic orbits followed by periodic solutions to the three-body problem of different masses predicting machine learning. Blue line: first planet; Red line: second planet; Black line: Third planet.

കുറിച്ച് About the author

Dr. Shijun Liao, Geotong University, Shanghai, Chair Professor, School of Marine, Marine and Architectural Engineering

Adjunct Professor in the School of Physics and Astronomy at Geotong University, Shanghai

Dr. Xiaomingli, Jinan University, Associate Professor, School of Mechanics and Architectural Engineering

Yang Yu, Shanghai Geotong University, Ph.D.